环境准备

Cuda对应图

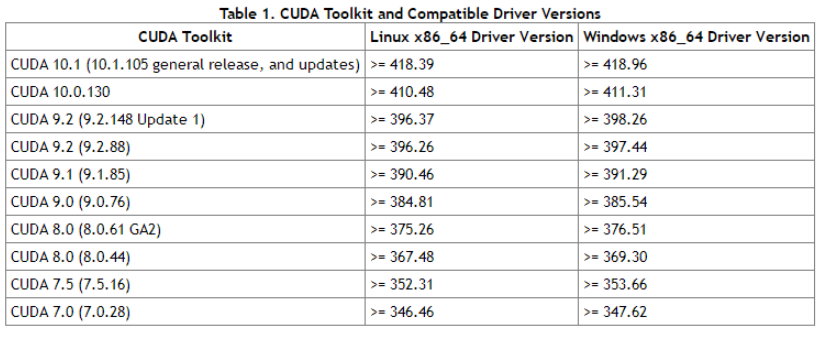
用Conda安装指定Cuda版本的Pytorch

1	conda install pytorch cudatoolkit=10.1 -c pytorch

安装多版本Cuda（用Pytorch框架不用安装Cuda）

下载安装

# 根据Cuda对应图下载指定版本的cuda，下载runfile文件,这里以10.1为例
wget https://developer.nvidia.com/compute/cuda/10.1/Prod/local_installers/cuda_10.1.105_418.39_linux.run
# 赋予runfile执行权限
sudo chmod a+x cuda_10.1.105_418.39_linux.run
# 执行安装,记住装过驱动了就别装驱动了，选项可以根据自己的需要进行选择
sudo ./cuda_10.1.105_418.39_linux.run
# 在用户主目录的.bashrc文件中添加（或修改成）以下两行，将执行库和cuda可执行文件写入环境变量
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/cuda-10.1/lib64
export PATH=$PATH:/usr/local/cuda-10.1/bin

使用软链接更方便切换版本

# 先将/usr/bin/cuda软链接指向指定版本
sudo rm -f /usr/bin/cuda # 删除软链接
sudo ln -s /usr/bin/cuda /usr/local/cuda-10.1 #重建软链接
# 修改环境变量如下
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/cuda/lib64
export PATH=$PATH:/usr/local/cuda-10.1/bin

每次切换版本只需要重建软链接就可以了。

训练技巧

模型参数初始化

普通梯度下降法（SGD,Batch梯度下降）

使用普通的梯度下降方法时，初始化模型时对参数进行归一化，以防止不同参数的scale不一样，部分参数在同等学习率下无法更新

自适应学习率梯度下降法法（动量法，RMSprop算法，Adam算法）

采用自适应学习率的梯度下降方法不需要对参数进行归一化，因为会根据不同scale的梯度进行学习率的缩放，最终稳步达到lLocal optimal

梯度下降优化方法

RMSprop算法

采用EMA（指数移动平均）来计算每次更新的梯度，公式如下：

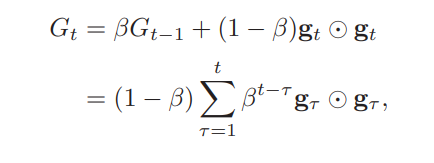
其中$\beta$为衰减率，一般取0.9；$G_t$就是多次梯度的指数衰减平均，其中时间越接近当前的梯度权重越高，时间越早的梯度权重越低。

其中参数更新差值（参数更新前后的差值，方向为负表示下降）计算如下：

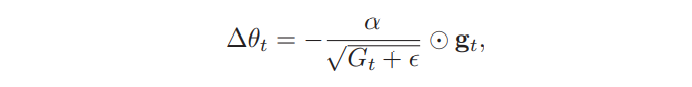
其中$\alpha$为初始学习率，比如0.001；迭代过程中每个参数的学习率随着$G_t$变化而变化，当EMA值较大时，学习率会变小，抑制更新，EMA值较小时，学习率会变大，加速更新，由此反复动态调节。

动量法

在物理上，动量是速度和质量的乘积，也就是和速度成正比；动量法就是用之前积累的动量代替真正的梯度，而把单词的梯度当作是梯度加速度。

在第t次迭代时，计算负梯度的EMA作为参数的更新量：

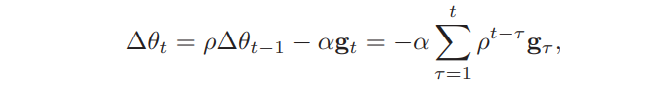
其中$\rho$代表动量因子，通常为0.9，$\alpha$为学习率；

每个参数的实际更新差值取决于最近一段时间内梯度的加权平均，当某个参数在最近一段时间的梯度方向不一致，其真实的参数更新幅度就会减小，起到减速作用，反之亦然。也就是说在反复震荡的时候可以减小梯度更新幅度（而不是学习率）增加了稳定性。

Adam（自适应动量估计）方法

动量法和RMSprop的结合，不仅用动量作为参数更新量，而且可以自适应调整学习率。

公式如下：

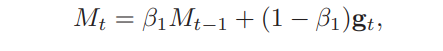
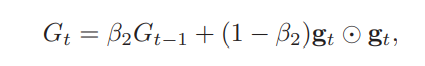
其中$\beta_1$和$\beta_2$分别为两个移动平均的衰减，通常取值为0.9和0.99，$M_t$为参数更新量，$G_t$为学习率衰减系数。

一般$M_0$和$G_0$一般都设置为0，迭代初期$M_t$和$G_t$的值跟真实均值和方差相差较大，被系数缩小了很多（特别是$\beta$接近1的时候），可通过以下公式进行修正：

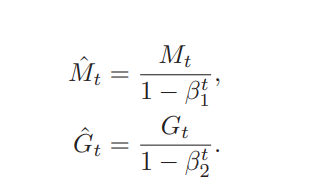
随着时间的累积，分母趋近为1，两值之间的差距基本上可以无视。

Adam算法的参数更新差值为：

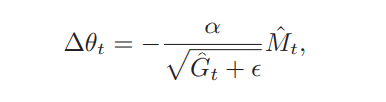
其中学习率通常设置为0.001。

参考文献：

《神经网络与深度学习》 – 邱锡鹏

feng's blog

深度学习笔记